The method was tested using both Monte-Carlo simulated and real data. To
simulate a histogram data set for testing we integrate sequentially the
Gaussian sum (5) in each bin for various D. Then a random normally distributed noise
with ![]() is added to each bin.
is added to each bin.
Our calculations show the excellent performance NP-PAM algorithm, in
particular, in resolving double peaks from the unimodal histogram.
The corresponding example is presented in Fig.1, where two peaks lying
apart only for one half of the bin-size were simulated for
![]() =0.1% of the mean amplitude value and signal half-width
equal to 2 bin-size (Fig.1-a). In Fig.1-b it is shown how NP-method
resolves both peaks and the accuracy of PAM is presented as the
distribution of deviations from modelled and estimated position of one of
these peaks. Combine NP-PAM algorithm reconstruct pulse positions with
accuracy better than 0.01 of bin size.
=0.1% of the mean amplitude value and signal half-width
equal to 2 bin-size (Fig.1-a). In Fig.1-b it is shown how NP-method
resolves both peaks and the accuracy of PAM is presented as the
distribution of deviations from modelled and estimated position of one of
these peaks. Combine NP-PAM algorithm reconstruct pulse positions with
accuracy better than 0.01 of bin size.
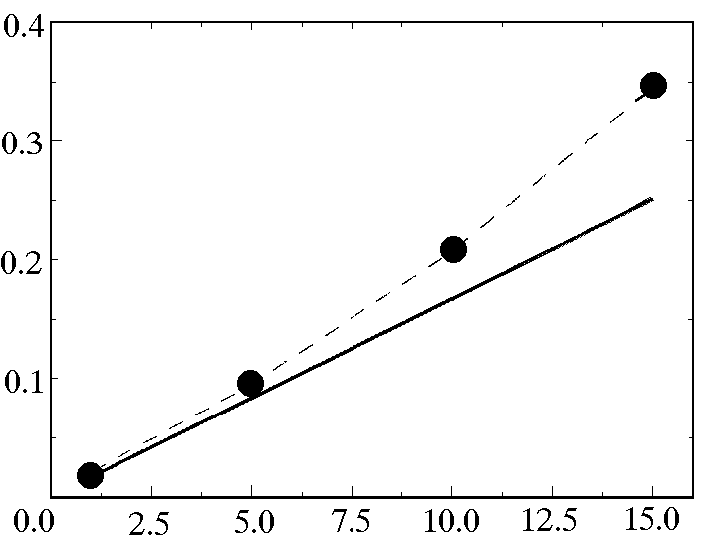
Fig.2 The signal RMS (black circles) and the
Cramer-Rao lower bound (4) as the function of the noise standard
deviation. On Y axis is ![]() , on X axis is
, on X axis is ![]() in [%].
in [%].
One can see
that for ![]() less than 10% PAM procedure reaches
almost its limiting accuracy.
less than 10% PAM procedure reaches
almost its limiting accuracy.
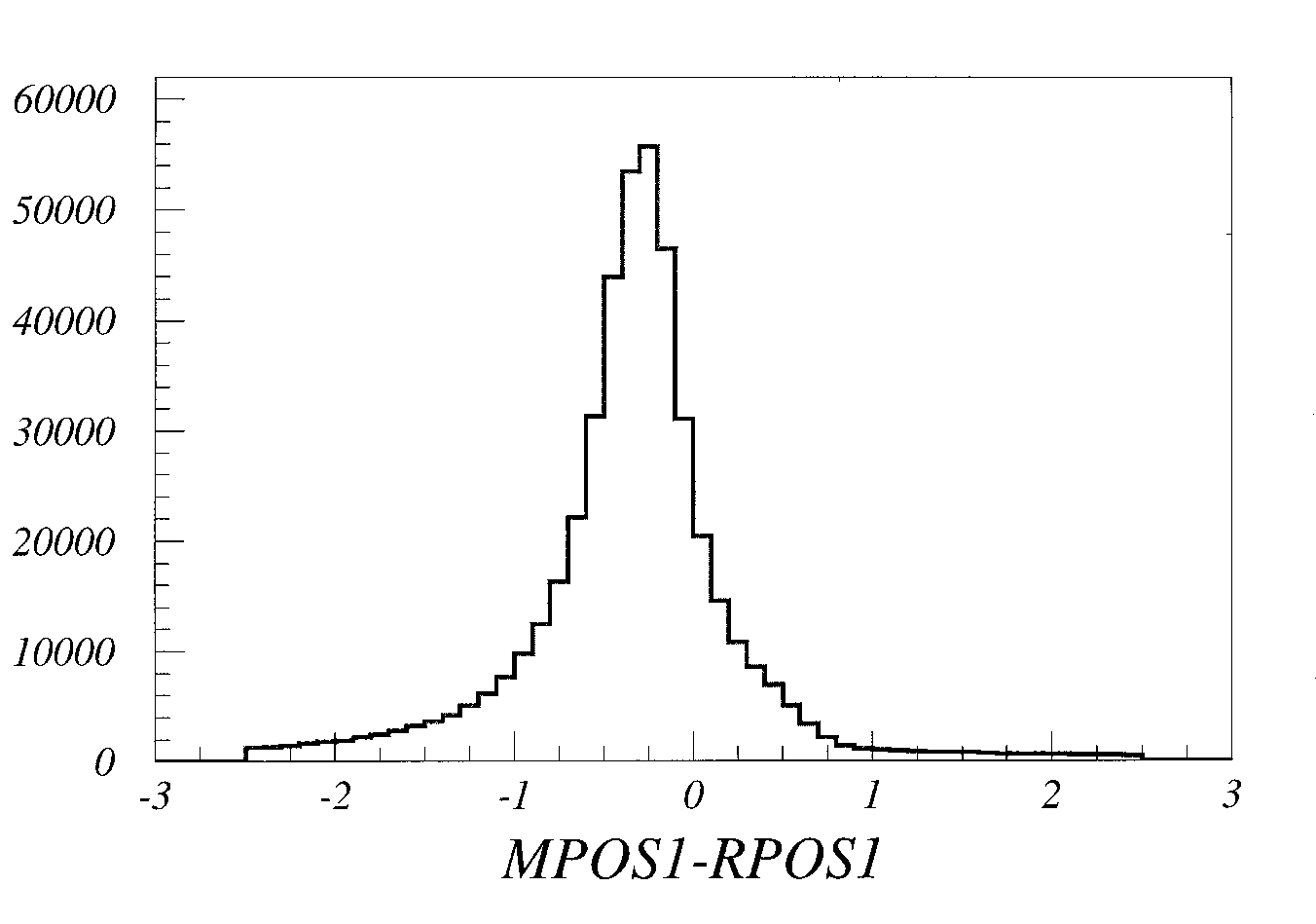
Fig.3 The distribution of differences of two pulse positions obtained by two methods (PAM and a conventional using the MINUIT program) for 160GeV/n Pb-Au data from CERES experiment [5].
Among 5000 events the only clusters were selected with the distance
between
pulses less or equal than signal shape half-width.
For ![]() over 10% the results are quite satisfactory.
over 10% the results are quite satisfactory.
Authors would like to thank Professor J.P.Wurm and Dr H.Agakishiev for the valuable help and providing the experimental data.