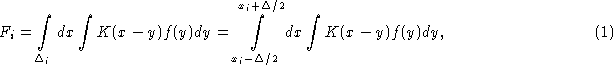
The non-parametric approach, also named the unfolding problem, is applied when the problem parametrization is unknown. Mathematically the problem is reduced to the solution of the following integral equation of the first kind
where the unknown function is f(y);SPMgt;0 and so-called instrumental
function K(x) is, in general, determined by a specific of the physical
problem. Our contribution to the problem is the explicit including to
the kernel K(r) the effect of the information loss due to the
histograming process. To take into account the finite size of our
histogram bin we substitute the kernel K(x) in (1) for the
convolution 
with the characteristic function
of the interval 
, i.e.
h(x)=1 for 
and 0 otherwise.
Although for continuous kernels this problem is ill-posed (see for
example [1]), however as it was there proved,
when one looks for a solution on a compact set the problem can be solved
for a sufficiently wide class of kernels including the convolution
. Due to always presenting noise there is the resolution
limit for close signals, which is non-improved of principle. That follows
from the well-known Shannon's theory on the maximum speed of the data
transmission via the channel having a noise. Such the limiting
superresolution factor is (see [2])
Here 
is the signal energy: 
and 
is the noise energy: 
where n is the number of experimental data points, and 
is
the variance of input noise.
If the signal-to-noise ratio is expressed in decibels
the approximate expression for the superresolution limit is
.
In the paper [3] the computer program package RECOVERY was described, which can reach the Shannon superresolution limit. The programs from the RECOVERY package are based on the maximum likelihood principle and they look for maximum of the likelihood function in the many-dimensional set of solutions, which is always a compact set. The RECOVERY code is accessible from the CPC Program Library. The results of non-parametric approach described in this paper was obtained by use the modified DCONV program from the RECOVERY package. Further we refer to non-parametric method as to NP.
