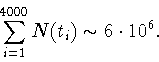The following is only a description of the parts of the RECOVERY
algorithm relating to the special features of the ![]() experiments. The detailed description of the algorithm and its applications
can be found in papers [7] and [8].
experiments. The detailed description of the algorithm and its applications
can be found in papers [7] and [8].
In ![]() experiments, scintillating counters detect the muon's decay
positron, the direction of which is correlated with the muon spin direction
at the time of its decay. The number of decay positron is histogrammed as
a function of the time taken to decay
experiments, scintillating counters detect the muon's decay
positron, the direction of which is correlated with the muon spin direction
at the time of its decay. The number of decay positron is histogrammed as
a function of the time taken to decay
The polarization function P(t) in Eq.(8) can only be uniquely
determined from the histogram N(t)
if all parameters N0, B and AMu are known.
We chose to pre-determine the parameters N0, B and AMu
using the crude standard ![]() analysis method (using Eq.(9) below)
and then use those values to extract the generalized P(t) from the
experimental N(t).
analysis method (using Eq.(9) below)
and then use those values to extract the generalized P(t) from the
experimental N(t).
For the first step of determining N0, B and AMu,
we use the fact that in temperature range 0.5 - 1.5 K the muonium
formation time t0 is less than the total histogram duration
![]() and for
and for
![]() ,
when all atoms of muonium
have been formed, the equation for histogram can be written as
,
when all atoms of muonium
have been formed, the equation for histogram can be written as
The system equation originating from the minimization of Eq.(10)
has a symmetric and positive-definite matrix. We solve this system by the
Cholesky decomposition method (square root of matrix) with the subroutines
CHOLSL and CHOLDC from the 2nd edition of the "Numerical Recipes" book
by W.H.Press et al [10]. These programs were modified for double
precision (
![]() )
accuracy. The use of the Cholesky decomposition
method for a symmetric and positive-definite matrix provides more stable results
than the Gaussian elimination method which does not use the symmetry properties
of the matrix.
)
accuracy. The use of the Cholesky decomposition
method for a symmetric and positive-definite matrix provides more stable results
than the Gaussian elimination method which does not use the symmetry properties
of the matrix.
With values for the parameters A,B,C and D we compute N0
and asymmetry coefficient AMu using the formulas
The polarization function P2(t) starts from the initial value
Traditionally another normalization is used
It is obvious in Fig.1 that the noise level in function P(t) increases
with t. This level can be easy seen from the
the fact that N(t) has a Poissonian distribution which results in
After these appropriate preliminary calculations let us go to the main problem of this paper: how to determine the muonium formation rate function n(t) in a model independent way, that is without assuming any particular theoretical form with fit parameters for the polarization function P(t).
Eq.(7) can be rewritten as
Eq.(15) is the Volterra convolution integral equation of the
first kind with the kernel
To solve this integral equation we use the program Dconv2 from
the program package RECOVERY. The program Dconv2 was originally
designed for the solution of the Fredholm integral equation with
fixed integration limits
The program package RECOVERY, which is based on the maximum likelihood method
(MLM), was chosen because this method attains the maximum possible resolution
enhancement for a given signal to noise ratio in the input experimental data
[7]. According to the MLM, the likelihood function
| (20) |
Consider the set of unknown values of the function
G0(yj), j=1,2,...,m as a vector in an m-dimensional space of
solutions. Each point in this space corresponds to one possible solution,
and the next step is to search for the likelihood function maximum
An explicit form of the likelihood function for the case of polynomial
statistics is given in review paper [12]. Poissonian
statistics are a special case of polynomial statistics.
If the data are described by Gaussian statistics, then the logarithmic
likelihood function is the square of deviation between the experimental
data ![]() and their approximation
and their approximation
![]() ,
i.e.
,
i.e.
The search for the likelihood function maximum is performed iteratively by the steepest ascent method which is a sign-inverted variant of steepest descent method. All explicit formulae of iterative algorithms for both polynomial and Gaussian input data statistics can be found in reference [8] and a full listing of the RECOVERY code in Fortran 77 is available from the CPC Program Library providing that person requesting the program sign the standard CPC non-profit use licence. The more sophisticated conjugate gradient method is used in this paper for maximization of the likelihood function.
The number of detected positron in one time bin in our measurements was about 103 - 104 and it is well known that for such large numbers of events Poissonian statistics are reduced to Gaussian. It follows from the Eq.(14) that the variance of input data P(t) is inversely proportional to the histogram values N(t) and the main subroutine MLG8 should be used together with the program Dconv2. This subroutine is designed for input data having the Gaussian statistics with non-constant variance (see part 2 of paper [8]).
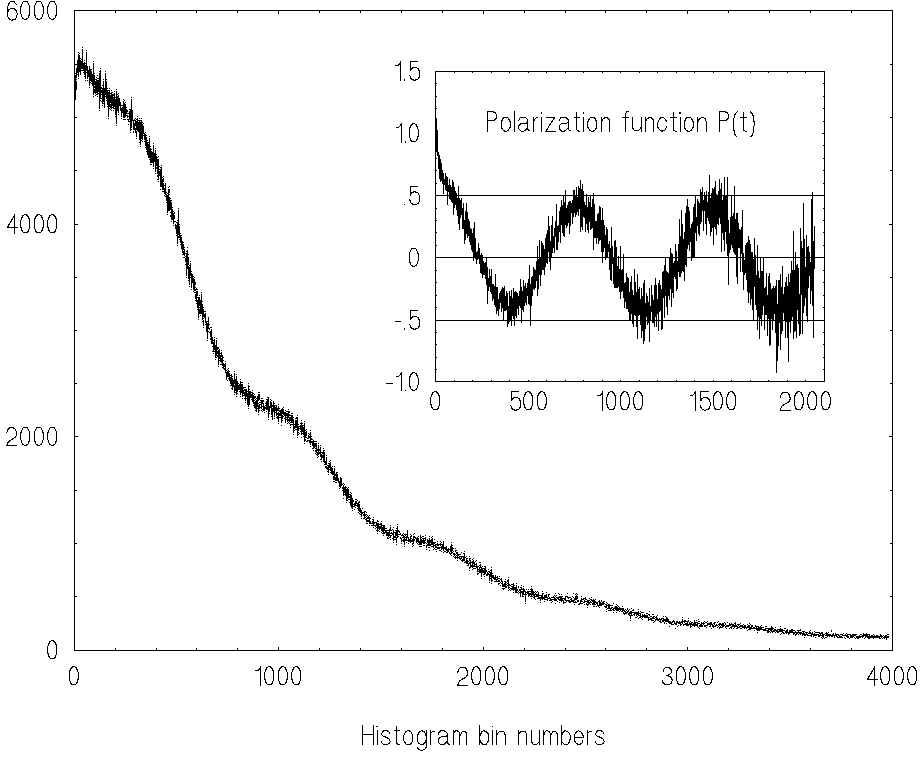
To demonstrate that our RECOVERY procedure is unbiased with respect
to the analytical form of formation rate function n(t) we choose two
trial functions with strongly differing shapes
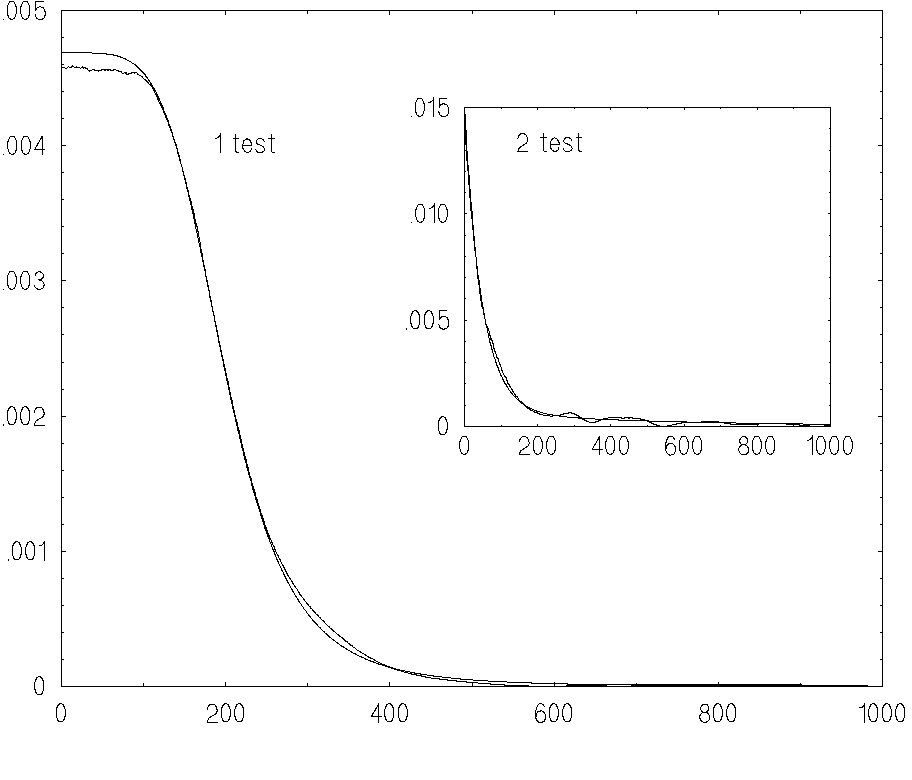
They are in good agreement. We
emphasize that the discrepancy between the estimate and exact solution
in Fig.2 does include two sources of errors: the systematic and
the statistical ones. The total error in Fig.2 is about 2%.
The statistical accuracy of the recovering procedure was also quantitatively
evaluated by a Monte Carlo procedure which was applied between 10 and 20 times
(see [9])
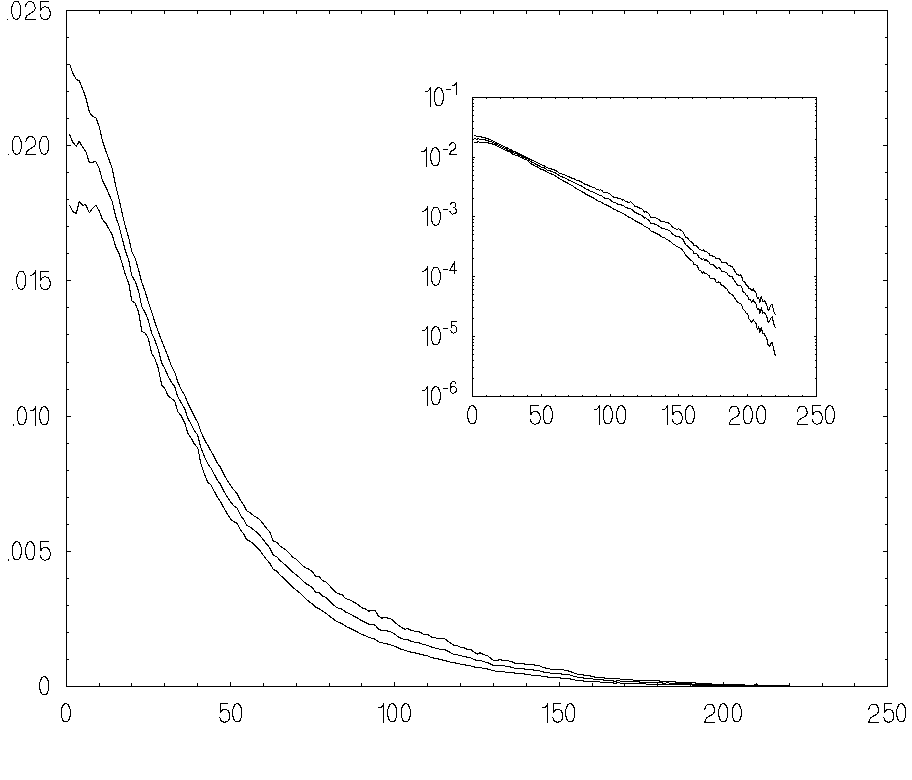
It is seen from this
figure that mean accuracy is less than 2% for total histogram statistics