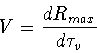Results

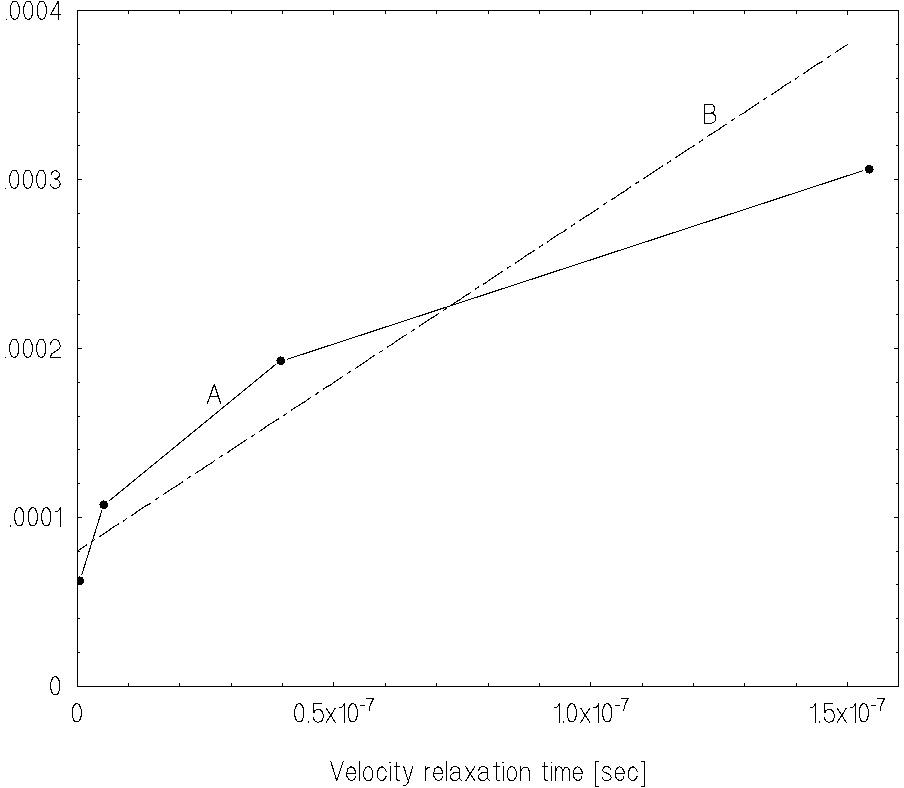
Fig.4 shows the muonium formation rate n(t) in superfluid helium over the temperature range

$$0.5K \leq T \leq 1.35K,$$ (24)

as extracted by our method.

Fig.4. Muonium formation rate functions n(t) in liquid He in the temperature range $0.5K \leq T \leq 1.35K$.

The muonium formation rate increases for time interval $t < 0.3~\mu s$ with decreasing helium temperature and the rate decreases for time $t>0.5~\mu s$. It is interesting to compare these results with the measurements of muonium precession amplitude published in paper [13], which makes it clear that the decreasing of A_Mu at large temperature results from the formation time

$$t_{Mu} \simeq (\gamma_{Mu}H)^{-1} \simeq 0.2~\mu s.$$ (25)

Here $\gamma_{Mu}= 1.404~MHz/Oe$ is the gyromagnetic ratio for muonium. The value n(0) increases in temperature range $0.5 \leq T \leq 1.35 K$ with reduction in helium temperature, but the integral value

$$A_{Mu} = \displaystyle\int_0^{t_{Mu}} n(t)dt$$ (26)

decreases.

Let us consider the function W(r) which is radial density distribution of muon-electron pairs. This function makes obvious physical sense for the Coulomb attraction of a muon and an electron in liquid helium in the viscous regime. This distribution function is appropriate when the ions have relaxed to their final local equilibrium and their relative velocity vector will be

$$V=-b\nabla \varphi,$$ (27)

where b is the mutual mobility and $\varphi$ is the electric field potential.

We will ignore for simplicity the space asymmetry of distribution function W(r), which was discovered in paper [14]. Then we obtain the equation

$$P(t) = 1 - 2\pi \displaystyle\int\limits_0^{r(t)}W(\xi)\xi^2d\xi.$$ (28)

instead of Eq.(3). Let introduce the new variable $\tilde{t} =bt$ to eliminate the mobility b from Eq.(27). If W(r) is independent of temperature, then both P(t) and n(t) should be universal for all temperatures. However we can see from Fig.4 that a scaling law is not the case, because as the temperature changes, the mobility changes by a few orders of magnitude, while the function n(t) values changes only in shape.

It can easily be shown that the velocity relaxation time

$$\tau_v = Mb/e$$ (29)

is much less than the muonium formation time above 0.7K. Hence it follows that the lack of the scaling law is connected to the shape of distribution function W(r). This function can easily be found from equations (3), (27) and (28)

$$W(r)= \displaystyle\frac{n(t)}{4\pi eb}=\frac{n(r^3/3eb)}{4\pi eb}.$$ (30)

The muonium formation time for a muon and an electron spaced initially at distance r apart is

$$t=\displaystyle\frac{r^3}{3eb},$$ (31)

which was substituted in the second equality in Eq.(31). The distribution functions $4\pi r^2W(r)$ are shown in Fig.5 for helium temperature range $0.7K \leq T \leq 1.35K$.

Fig.5. Radial disribution functions $4{\pi}r^2 \cdot W(r)$ for helium temperature range $0.7K \leq T \leq 1.35K$.

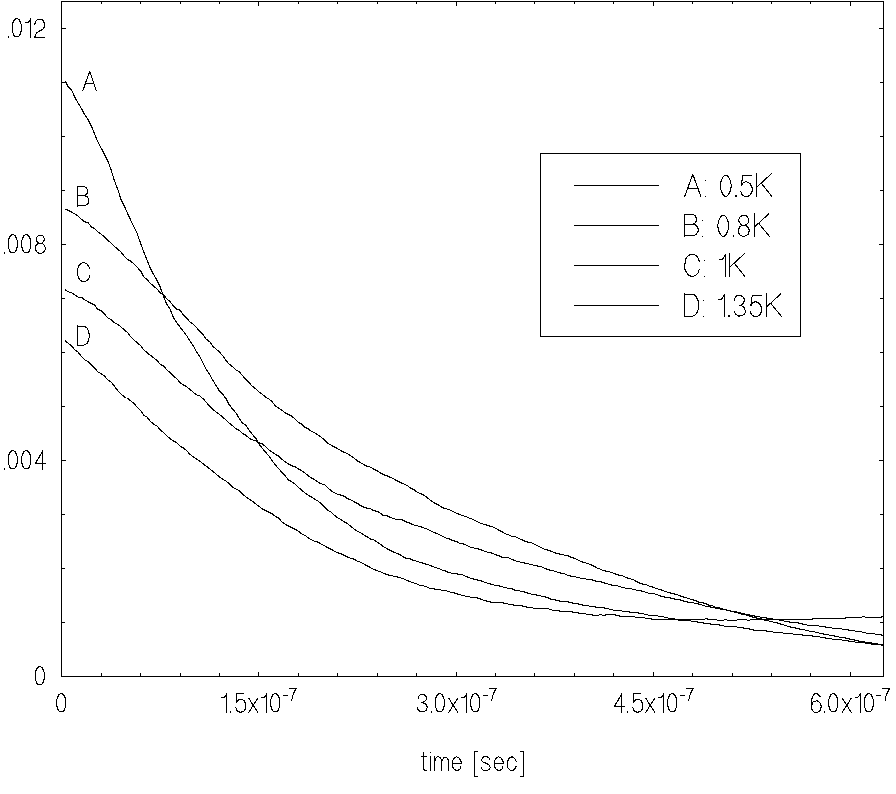
It is seen from this figure that both the mean and the dispersion of the distance between muon and electron pairs increase as the helium temperature is reduced. This follows by virtue of increasing mobility for particles in superfluid helium. The thermalization process in normal liquids are completed by a time of 10^-12 to 10^-10 s because of elastic phonon interactions. In contrast there is a gap $\delta E=8K$ in the superfluid helium excitation spectrum [15] which results in an anomalously high mobility of impurity particles, such as muons. As the energy of particles is reduced to less than 8K, the velocity relaxation time $\tau_v$ rises greatly. The positions of the maximums in the Fig.5 correspond to mean distances between muon and electron and their displacement is determined by dispersion of particles over the time $\tau_v$.

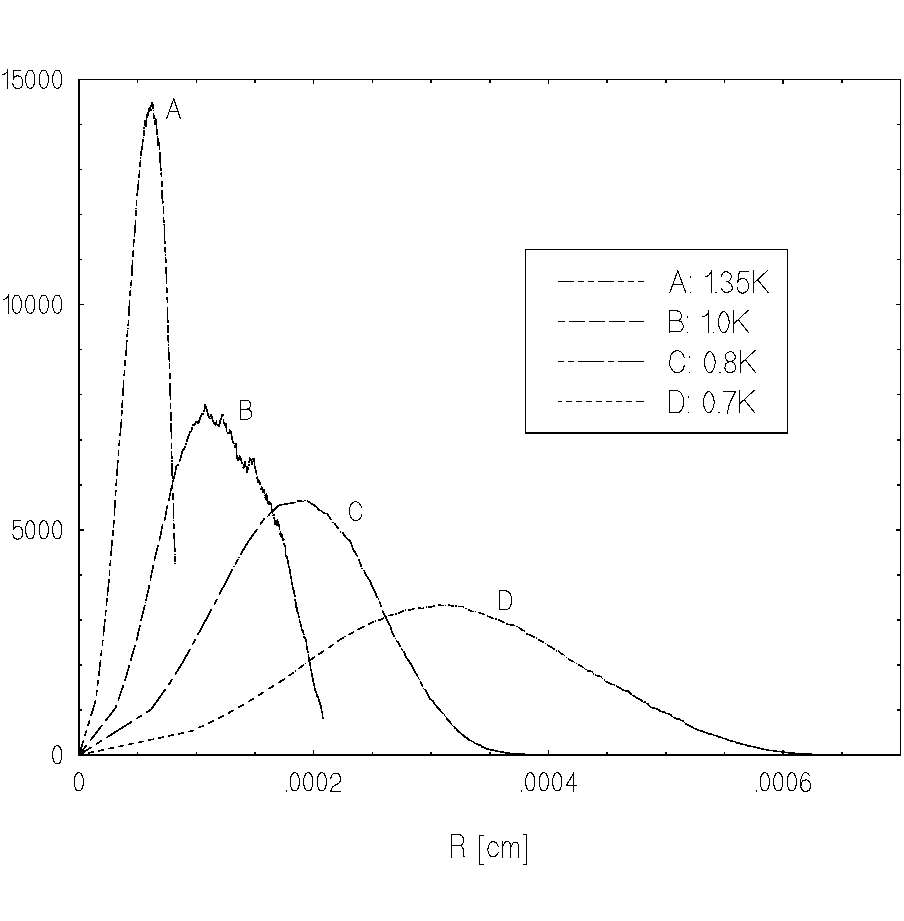
The dependence of the mean distance R_max on the relaxation time $\tau_v$ is presented in Fig.6. It is seen from the figure that dispersion speed

$$V=\displaystyle\frac{dR_{max}}{d\tau_v}$$

is close to the Landau critical velocity V_L=58 m/s in accordance with the theory of impurity particles movement in superfluid helium [16].

Fig.6. A: mean distance between muon and electron in a pair versus the function of velocity relaxation time $\tau_v$ derived from the data, presented in Fig.5
B: the straight line is corresponded to the Landau velocity V_L=20 m/s.